电容'完全'充放电时间公式的简单推导
问题引入
高中的通用老师曾在课上讲解电容时说,电容的完全充放电时间(T)等于充放电路径上的总电阻(R)乘以电容(C)
听到此处我觉得有些疑惑:
- 充电的电压在充电过程中同样是一个重要要素,为何此处与之无关?
- 理论中,电容并不能完全充放电,电容的电势差只能无限趋近于输入的电势差,这里所说的完全充放电恐怕不够严谨
- 常见的物理公式中,有相当一部分的公式存在一个
不讲道理的常数,例如在库伦力和电荷所带电荷大小与距离的公式其中库伦常数k值为 8.99 * 10^9 ,电容的充放电时长公式就没有这样的常数吗
毕竟老师讲课要以让所有人听懂为目的,有时牺牲严谨性也是无可奈何的
鉴于本人当时并无条件进行实验,故采取理论分析的方式来探究其中的疑点
理论分析
问题简化
首先假定我们所要研究的是如下的简单电路,并且仅仅考虑充电的情况: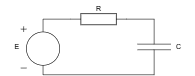
其中E为电源电动势(假定电源是理想电源,电动势恒定),R为充放电路径上的电阻大小,C为电容本身的电容大小
记过程中电路中的电流为I(t),电容的电势差为U(t),电容所带电荷量为Q(t),经过的时间为t
并且t=0时,U(0)=0,Q(0)=0
计算过程
常见的微分方程,假设
注意到
所以
将Q(t)带入微分方程中,得到
解得
从而
进一步解释
刚才我们得出了 电容的电势差U(t) 随时间变化的计算式,但是这还没有解决我们的疑惑
为了衡量电容器充电的程度,我们引入电容电势差和输入电势差之比η
而在我们的简化的模型中:
这个函数有如下的特征:
- 定义域为
- 在定义域内单调递增
可见,完全充放电的情形,即
BUT,实际的运用中,我们不需要那么严谨,只要电容器可以被近似地认为“完全”充放电,讨论充放电到某一程度的时长就是有意义的
假定人对于”完全充放电”的标准是
那么电容器恰好达成充放电标准的时间T满足
解得
你也许发现了,我篡改了完全充放电的定义但是这不重要,不是吗?
这下我们离结论很近了!我们的分析表明
而且不难发现:
| T和R·C的关系 | |
|---|---|
| 63.21% | T=RC |
| 86.47% | T=2RC |
| 95.02% | T=3RC |
| 98.17% | T=4RC |
| 99.33% | T=5RC |
| 99.99% | T=9.3RC |
这说明公式T=RC应该加上一个无量纲常数,至于这个常数的取值,则看你在实际运用中的需要了
例如:
在以电容器为计时器的震荡电路中
如果高电位为
低电位为
那么单次充电或者放电的时长t=0.693RC (
小结
以上的分析中,我们解答了自己的疑惑
也许你会追问:B你不是没有分析放电的情况吗?
我认为,放电的情况和充电的情况没有本质区别,两者会得出相同的结论,因此没有做进一步的计算绝对不是因为我懒
Have A Nice Day!