舵轮底盘

Brief

舵轮底盘即使用舵轮作为底盘动力轮的底盘。这种轮子由只控制轮子方向的舵向电机和提供动力的动力轮电机控制。实际中我们是使用一个GM6020作为舵向电机，一个3508作为动力轮电机来控制一个舵轮。
根据使用舵轮和无动力的万向轮的数量比，舵轮底盘有全舵轮底盘和半舵轮底盘的区别。对于不同兵种，其底盘功率限制的规则各不相同。例如，底盘功率更大的哨兵就可以选用全舵轮底盘，而底盘功率较小的英雄和步兵可能需要选用半舵轮底盘。对于底盘在平地上运动的情况，全舵轮和半舵轮的运动学解算并无区别。

理论计算

底盘运动学逆解算

已知底盘目标平动速度和目标自旋速度，容易得到每个舵轮的目标平动速度

那么对于编号为的舵轮来说，6020应该转向（或）;3508的转速应该为

为什么6020目标角度和3508目标速度有多种取值？
这是因为我们加入了接下来要介绍的最小角优化。
如果不加入下面所介绍的优化的话，那么6020的目标角度就是, 3508的转速就是

什么是atan2?
atan2() 是 C 标准库 <math.h> 中的一个函数，用于计算两个参数的反正切值。这两个参数表示一个点的 y 坐标和 x 坐标，atan2() 函数返回从 x 轴到点 (x, y) 的角度，以弧度为单位。
这个函数比单独使用 atan() 函数更强大，因为它考虑了 x 和 y 的符号，从而可以确定正确的象限。

另外作一个说明,此处应当取落在范围中的值.它用来表示原目标角度的反方向.在这篇文章中,它不应该被认为有同时取到两种不同的值的可能

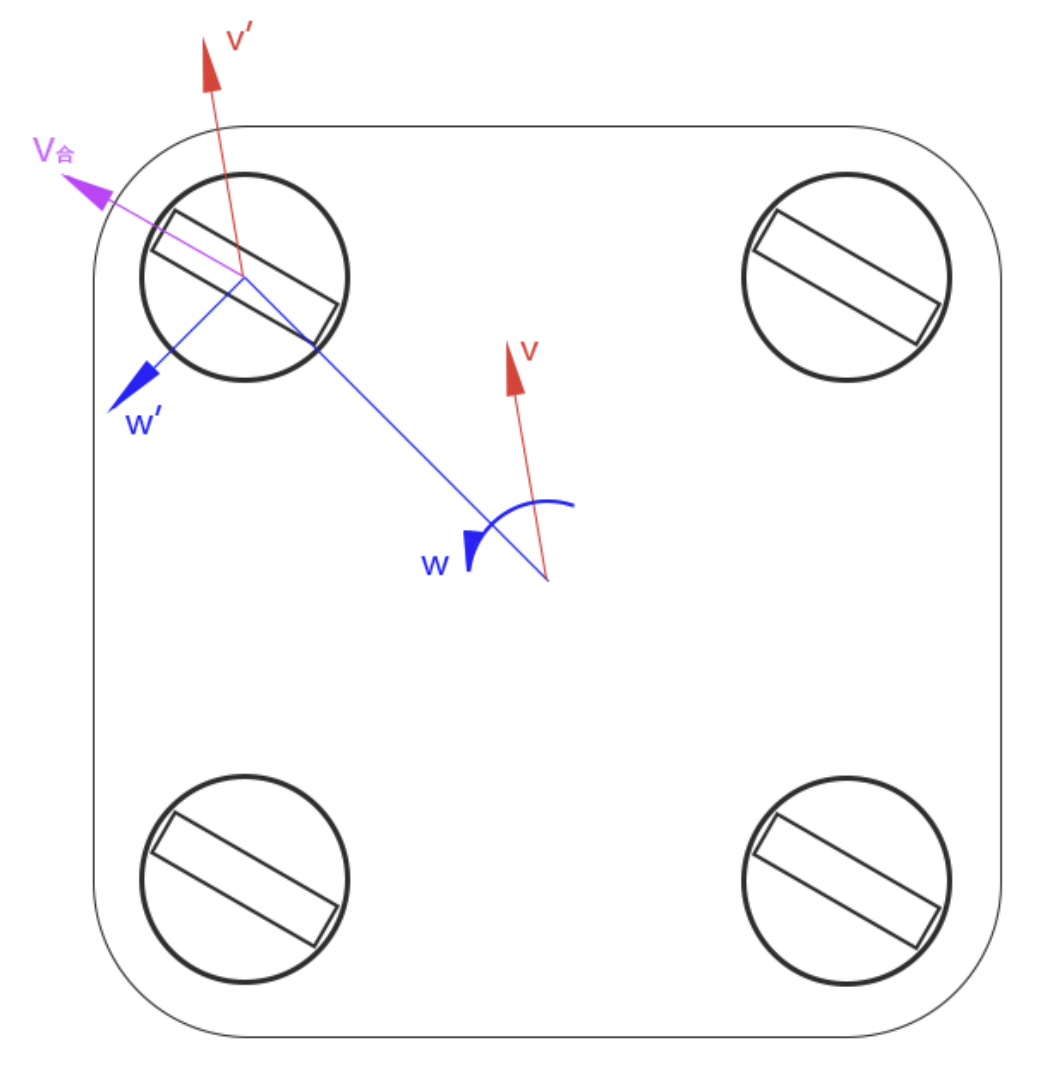
“最小角”优化

不难发现,当舵轮的方向和速度取值和取值的作用效果是相同的

不妨想象这样的情形：底盘原先正在向正前移动，突然收到了向正后方移动的指令。按照一开始的解算结果，舵向轮将旋转180°到正后方，然后底盘才能真的向正后方移动。很显然，如果直接让动力轮反向旋转而舵向轮不动，底盘将更快的响应指令。
类似的，如果可以减少舵向轮所转过的角度，就可以提高底盘的响应速度。

记舵向轮的从当前角度转到目标角度所需转过的角度（以电机正向转动方向为正）为舵向轮的偏差角度

余弦优化

通常情况下，动力轮的响应速度会比舵向轮更快，这会造成舵向轮在旋转时动力轮已经达到了目标速度。
理论上，这会造成在垂直于目标速度的方向上有速度，造成一段不期望出现的位移。
将动力轮的目标速度乘以可以抑制这种情况
在添加了这种优化的情况下，动力轮的速度不再需要考虑其符号，因为余弦已经有符号了。动力轮的目标速度总为

提醒
本文的代码没有使用余弦优化
（写作时间原因）

代码实现

提醒
代码仅作参考，实现舵轮底盘还存在其他人的写法

警告
本篇使用了作者本人魔改过的pid代码，引入了前馈
经过测试，对于舵轮底盘的实现，引入前馈是负优化

舵轮功能实现

我将一个舵轮视作一个对象Motor_Node。这个对象包含一个3508对象，一个6020对象，以及控制两个电机的PID和它们的目标值和输出值

// chassis.h
typedef struct{
    Motor M3508,M6020;
    int16_t spin_speed;     //M3508目标转速
    int16_t angle;          //M6020目标角度
    int16_t out_3508;       //M3508输出电流
    int16_t out_6020;       //M6020输出电流
    SinglePID_t PID_3508_speed,PID_6020_speed,PID_6020_angle;
}Motor_Node;

当舵轮收到运动学解算的结果时，会根据最小角优化的算法得到两个电机实际的目标角度/目标速度。
然后将目标值塞给对应的PID，得到两个电机各自的输出电流
最终将输出电流值发送出去

// chassis.c
void Motor_Node_FillData(Motor_Node* node);

float error_angle(float target, float current){
    float error;
    error = current - target;
    error = error > 180 ? error - 360 : error;
    error = error < -180 ? error + 360 : error;
    return error;
}

void Motor_Node_Calc(Motor_Node* node, int16_t speed, int16_t angle){
    float err;
    err = error_angle(angle, node->M6020.Data.Angle);
    if ( ABS(err) > 90 ){
        angle = angle >= 180 ? angle - 180 : angle + 180;
        err = error_angle(angle, node->M6020.Data.Angle);
        speed = -speed ;
    }

    node->spin_speed = speed;
    node->angle = angle;

    node->out_3508 = BasePID_Calc(&node->PID_3508_speed,node->spin_speed,node->M3508.Data.SpeedRPM);
    int16_t M6020_speed = BasePID_Calc(&node->PID_6020_angle,0,err);

    node->out_6020 = BasePID_Calc(&node->PID_6020_speed,M6020_speed,node->M6020.Data.AngleSpeed);

    Motor_Node_FillData(node);
}

void Motor_Node_FillData(Motor_Node* node){
    MotorFillData(&node->M3508, node->out_3508);
    MotorFillData(&node->M6020, node->out_6020);
}

底盘功能实现

全舵轮底盘有4个舵轮，因此定义4个舵轮对象作为全舵轮底盘。
得到底盘的目标运动数据后，调用底盘运动学解算函数并把结果分发给每个舵轮对象

// chassis.c
void Chassis_Calc(float vx, float vy, float w){
    float x[4],y[4];
    x[0] = vx + w * 0.7071f ; y[0] = -vy + w * 0.7071f ;
    x[1] = -vx + w * 0.7071f ; y[1] = vy - w * 0.7071f ;
    x[2] = -vx + w * 0.7071f ; y[2] = vy + w * 0.7071f ;
    x[3] = vx + w * 0.7071f ; y[3] = -vy - w * 0.7071f ;

    for (int i = 0; i < 4; i++){
        float spin_speed = Sqrt( x[i] * x[i] + y[i] * y[i] );
        float angle;
        if ( x[i] == 0 && y[i] == 0 ){
            angle = Nodes[i].angle;// 无输入选择维持当前角度
        }
        else {
            angle = atan2f( y[i] , x[i] ) * 57.29578f;
        }
        Motor_Node_Calc(Nodes+i, spin_speed, angle);
    }
}

▶

不符现实的解算结果？

如果你自己做过一次运动学解算，你或许会发现你算出的结果和我的代码是对不上的:

x[0] = vx + w * 0.7071f ; y[0] = -vy + w * 0.7071f ;
x[1] = -vx + w * 0.7071f ; y[1] = vy - w * 0.7071f ;
x[2] = -vx + w * 0.7071f ; y[2] = vy + w * 0.7071f ;
x[3] = vx + w * 0.7071f ; y[3] = -vy - w * 0.7071f ;

这确实是一个令人费解的情况。导致这种情况的原因可能是舵轮的坐标系和底盘的坐标系不同
进行运动学逆解算时，我们默认了舵轮和底盘处于相同的坐标系中。
但是实际中，由于为舵轮做初始化时，舵轮的初始化情况可能各不相同，甚至不同的电控同学会实现出不同的初始化
这可能是出现这种情况的原因

我的解决办法是，架起舵轮底盘，使其离地，调整解算结果中的符号，并观察结果是否符合现实需求

—END—

---

引用：
C 库函数 - atan2()，菜鸟教程