重生之我在RM调试PID
引入
PID即:Proportional(比例)、Integral(积分)、Differential(微分)的缩写。顾名思义,PID控制算法是结合比例、积分和微分三种环节于一体的控制算法
PID控制的实质就是根据输入的偏差值,按照比例、积分、微分的函数关系进行运算,运算结果用以控制输出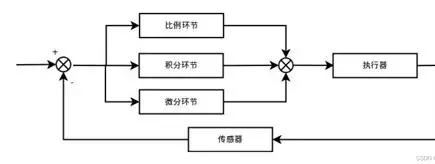
偏差
偏差即预定目标和当前状态之间的差值
我们设 预定值target是我们希望系统平衡时传感器的返回值
传感器实时返回的数值为measure
那么根据偏差的定义,我们可以得到偏差的计算式:
其中error为我们所求的偏差值
比例算法
成比例地反映控制系统的偏差信号,偏差一旦产生,立即产生控制作用以减小偏差。
比例算法的核心思想非常简单:离目标越远,就应该调整的越快
我们举 量取1L水的例子来说明
如果桶里面只有 10ml 水 ,那么你倒水的时候就会哗哗的往里面倒
而如果此时 桶快满了 ,你为了不倒多了,你就会选择慢慢的向下加
将这样的思想抽象成数学语言:
记比例算法的输出值为 P
那么 error 越大 , P就应该越大
即
其中 比例系数
积分算法
积分环节的作用,主要用于消除静差提高系统的无差度。
定义
积分算法是对比例算法的补充
还是量取1L水的例子,但是这次桶破了一个洞:
为了方便说明,不妨假设每秒的漏水为
,
你还是用比例算法的思想去倒水
然而在你加水加到了
这是因为此时你加水的速度是
和漏水的速度持平
如果你可以关注到水位一直都在
记积分算法的输出值为I,那么:
即
其中积分系数
离散化
显然,
积分算法的理论计算式离散化后可以用下式计算:
用C++实现:
1 | |
积分限制
引入积分算法后可能出现以下情况:
- 以电机为例,在电机的启停或设定值大幅变化时,系统在较短时间内产生了很大的偏差。此时积分迅速积累,就会造成控制量输出远远大于电机的极限输入控制量,从而会引起很大的超调,甚至会产生震荡。
- 积分饱和:当系统一直存在一个方向的偏差时,积分会不断增大,会造成控制量进入饱和区,一旦出现反向的偏差时,需要很长时间才能推出饱和区,而去响应反向偏差。也以电机为例,电机在积分饱和时,电机响应延时较大,会出现电机超出目标位置,需来回调整数次才能稳定。
此时就有必要限制积分算法的输出
如果
1 | |
积分分离
积分分离同样是一种避免过调的手段
既然积分算法的目的是消除静差,而且会在偏差值过于大的时候异常运行,那么不妨对积分算法做这样的限制:需要积分算法的时候再开启积分算法,不需要就关闭
设定积分控制阈值
微分算法
微分环节的作用能反映偏差信号的变化趋势(变化速率),并能在偏差信号的值变得太大之前,在系统中引入一个有效的早期修正信号,从而加快系统的动作速度,减小调节时间。
定义
微分算法同样是对比例算法的补充
这次的例子换成在手指上面立筷子吧
立筷子还不简单,你轻易的让筷子保持了竖直
正当我们放松的时候,一阵阴风袭来,把筷子稍稍吹歪了
只用比例算法?
筷子才歪这么一点,我都不需要怎么动哎
然后很快筷子就倒了加上积分算法?
本来筷子是保持平衡的,也就是此时积分算法能起到的效果和比例算法没有什么差别了
看来我们需要新的方法
立筷子之所以容易失败,是因为筷子只要有一点偏差,如果不迅速的加以修正,筷子就会快速的倒下
如果在
问题就可以迎刃而解
注意到微分是衡量瞬时变化率的很好的数学工具,于是我们可以写出:
即
其中微分系数
离散化
同样的,由于
用c++实现:
1 | |
微分先行
在某些给定值频繁且大幅变化的场合,微分项常常会引起系统的振荡。这是因为我们的微分项是对偏差值
明明实际值没有多大变化,微分项没理由发生突变啊。那只对实际值微分不就好了
综合使用
使用
总输出值的理想计算式:
如果全部带入:
离散化后可以用C++实现
1 | |
1 | |
调试参数
VOFA+ 上位机
VOFA+是一个直观灵活强大的上位机。它可以帮助我们显示调试过程中参数的图像。
要使用vofa+,你首先得安装它。这个软件功能是免费的,给作者爆米则可以更改这个软件的皮肤。
VOFA+ 参数设置
打开VOFA+,可以看到一个简洁的界面:
- 左上角的圆点表示和串口的连接状态,单击可以切换是否和串口连接
- 灰色-关闭连接
- 蓝色常亮-连接上串口但是没有数据收发
- 蓝色快速闪烁-正常进行数据收发
- 左侧侧边栏有三个按钮
- 协议和连接
- 数据引擎: 选择
FireWater模式,发送数据的格式可以看协议概览 - 数据接口:选
串口 - 端口号: 需要选择连接了TTL-USB的电脑端口,如果不会判断那就插拔TTL-USB,会变更的端口就是正确的端口
- 波特率:需要和设置的串口波特率一致。如果你没有修改过串口波特率那就使用默认的
115200即可 - 数据流控,校验位,数据位数,停止位数:同理,和串口的设置保持一致,如果你没有改过那就使用默认的
- 数据引擎: 选择
- 命令 - 我们一般用不到这个
- 控件 - 可以选择需要的控件加入到标签页中
- 协议和连接
- 中间上半部分是标签页区,可以摆放组件,比如图中的摆放了一个波形图组件
- 中间下半时数据流显示区,只要把
HEX切换为Abc就可以(十六进制显示切换为字符串显示) - 右侧是数据区,显示传回的不同的数据项
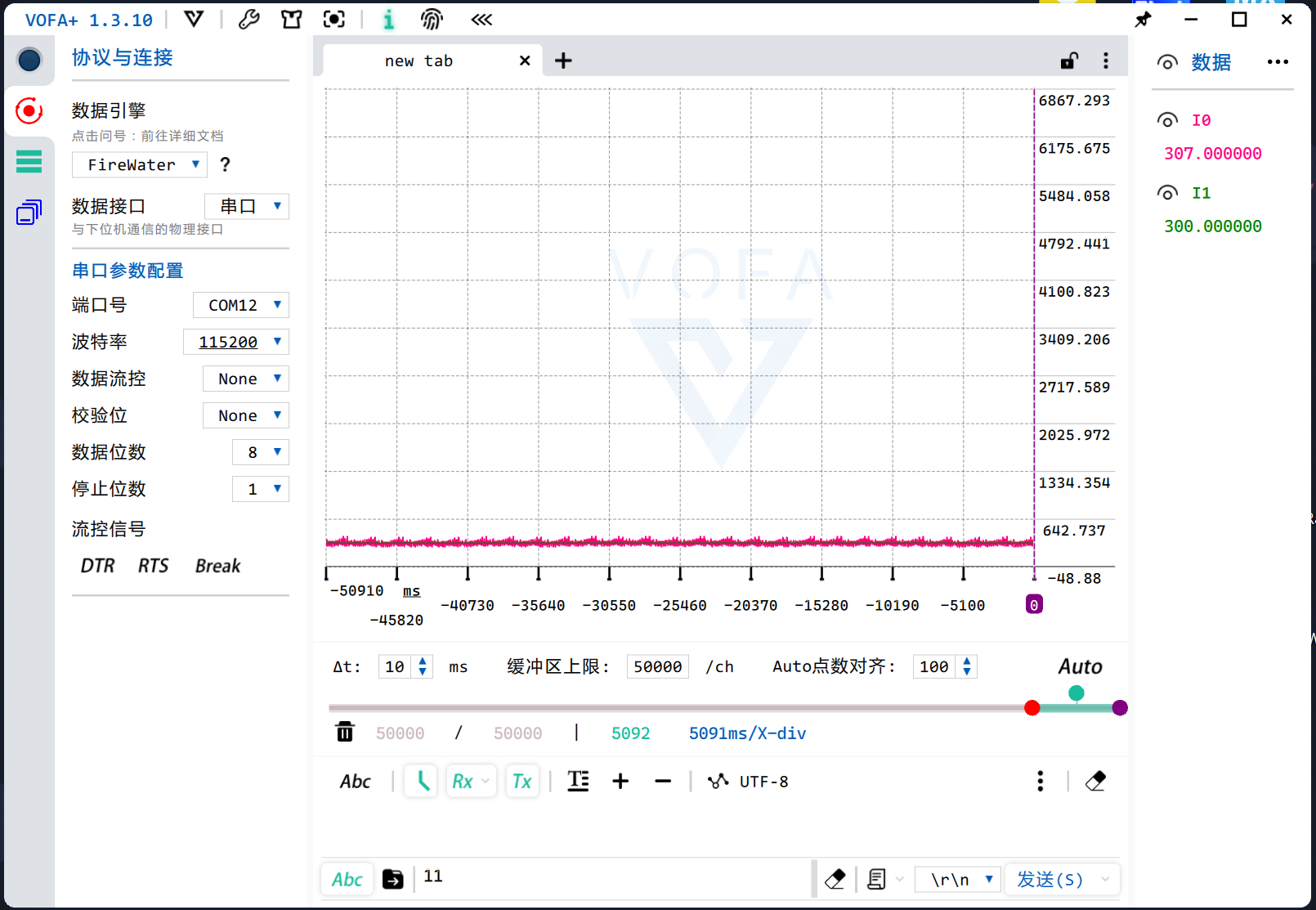
代码适配
串口发送数据的代码是从学长那里继承来的,我实际使用的有一些不同(原文见文章末尾参考部分)
值得提醒的是,数据发送给上位机的方式是DMA,请务必确认有无在CubeMX中打开对应串口的DMA
在项目中添加文件ano_vofa.h和ano_vofa.c,然后复制以下的文件内容
1 | |
1 | |
这样就可以使用函数UsartDmaPrintf(UART_HandleTypeDef *uartx, const char*format, ...)来便携地实现数据发送了
使用此函数的方法类似printf,比如:
1 | |
这样VOFA+正常接收到数据时会识别出两组数据
千万不要热插拔
热插拔指的是在正在传输数据时断开电脑和TTL-USB(或者烧写器)的连接
这一行为会导致 TTL-USB 发送数据的状态未解除,不能再进行正常的数据发送
表现形式为连接后VOFA+的蓝灯常亮不闪烁
解决方法
完全断电TTL-USB (即同时断开电脑连接和电源供电)
之后可以正常使用
超参数调试
超参数,这里指k_p,k_i,k_d三个参数。它们难以通过数学计算得出,基本上只能通过玄学经验来试出来
不过调试超参数还是有方法可依的
STEP.1 从PD开始调节
禁用I算法和D算法(就是让k_i和k_d等于0)k_p从一个较小的值开始调试(比如k_p = 0.4)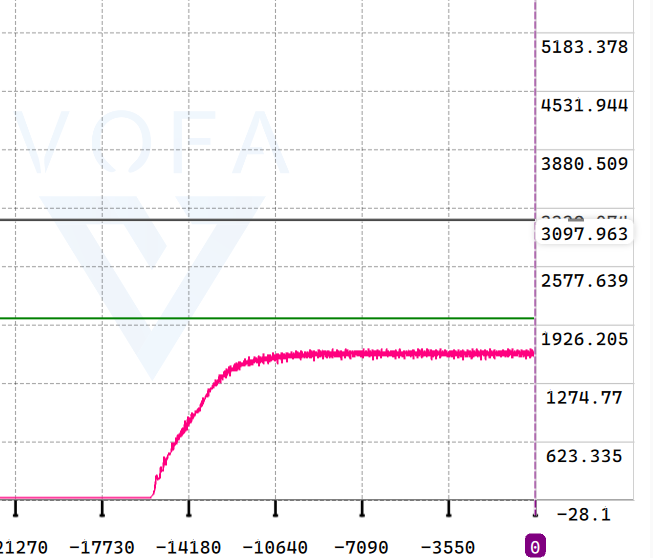
然后逐步提高k_p的值,直到接近恰好没有发生过调的临界点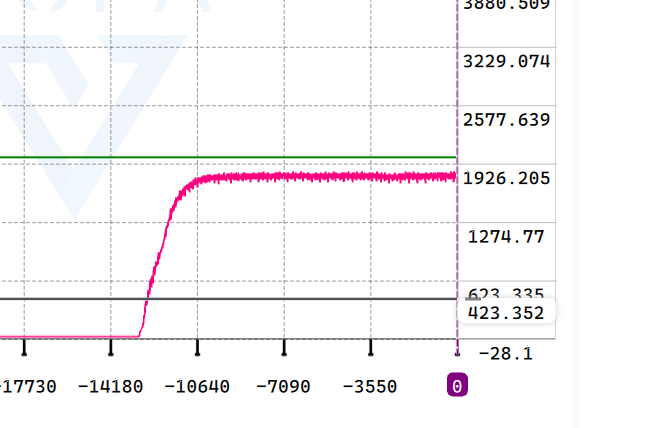
如果希望更快响应,可以让k_p更大一点,发生轻微过调后,加入d算法
由于本实验不是非稳定平衡系统,所以D算法不是必须的
- 稳定平衡
稳定平衡是即使受到扰动也会自行回归平衡状态的系统
最典型的例子是放在凹弧面底部的小球,这个小球即使偏移了底部的位置,也会自发回归平衡状态 - 非稳定平衡
非稳定平衡是受到扰动会无法自发回归平衡状态的系统
最典型的例子是放在凸弧面的顶部的小球。小球恰好在凸弧面顶部时是恰好平衡的,但是只要受到扰动,就会从顶部滚落,自发远离平衡状态
在实际中要实现这种平衡,必须在外部干预,比如使用PID算法来控制
平衡步兵就属于这种系统 - 恒平衡
恒平衡是不论处于何种状态都可以平衡的系统
一个放在水平平面的小球,无论怎么被扰动,都处于水平面上。在这个系统中,小球既不会有“自发回归”的趋势,也不会有“自发远离”的趋势
STEP.2 加入I控制,消除静差
完成上一步的调节后,逐步增加k_i的值,提高I算法控制的权重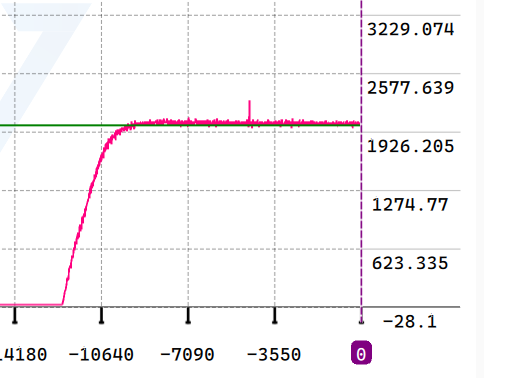
可见加入I算法后静差几乎消失,被控量曲线能够较好地贴合目标曲线k_i应该略小于恰好不发生过调的临界位置,过小会导致消除静差的过程过慢
下面是发生了过调的反例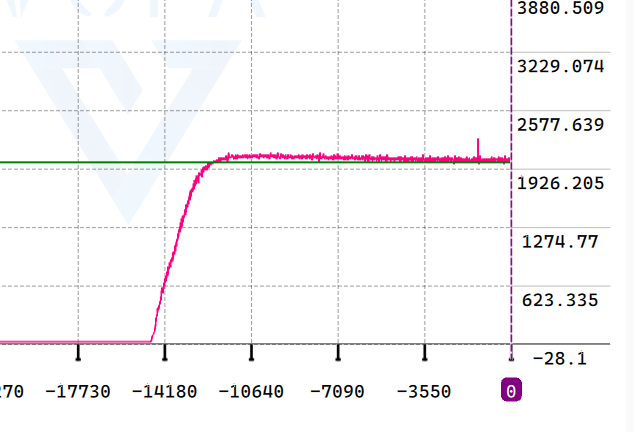
STEP.3 测试PID控制的跟随能力
实际使用时target值很少会有不改变的情况
在控制过程中频繁大幅度地改变target值,来观察曲线的跟随能力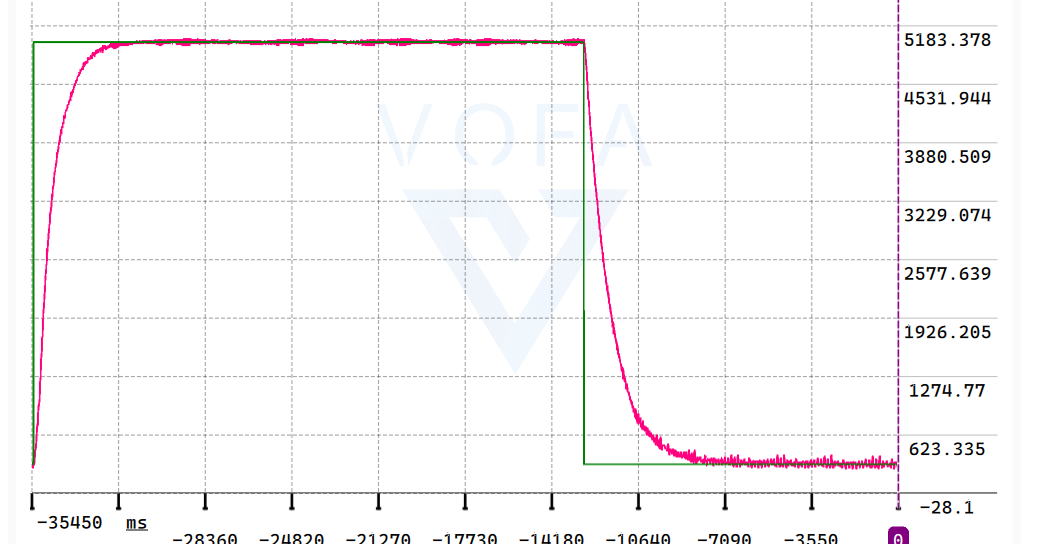
—END—
参考:
从不懂到会用!PID从理论到实践~,华南小虎队,BV1B54y1V7hp
【中科大RM电控合集】PID接口与电机闭环控制编程,TrojanGeneric,BV17m4y1L7E5
学会PID-基于板球平衡系统-初中基础就能听懂的简单讲,程欢欢的智能控制集,BV1xL4y147ea
图文详解PID调参&积分分离PID控制算法,宁静致远2021
CUBOT电控培训文档